先ず海(隗)より始めよッッ!!
↑今回の成果
私、予測たけし(以下、予測T.K)は圧倒的技術力を持って
世の中にはびこるギャンブルを根絶すべく
『競艇の完全予測技術の確立』を目指し、邁進してきた。
しかし、その成果はtwitterに記載の通り
凄惨たるものである(たぶん勝率0%)。
この要因として、競艇の実態を(ルールすら)知らずに
AI技術による予測に依存しすぎたことにあると考えられる。
つまり、今後予測レベルを向上するためには
競艇における素過程の理解は避けられない課題であると言える。
そこで、予測T.Kの技術力を活かして、
競艇予測における革新的アプローチを披露したい。
それこそが、
物理モデルによる競艇予測であるッッ!!!
、、、、、。
まず競艇における重要な要素となる
波の動きを再現する物理モデルの開発に着手した(制作約1.5日)。
先ず海より始めよう、、!
海モデルの構想1:支配方程式(面倒なら飛ばしてください)
波の物理現象をモデル化することを考えた際に、
まず頭に浮かんだのは、津波の浸水シミュレーション技術だ。
調べたところ、
”津波浸水想定の設定の手引き V2.10 2019年4月”という資料が
国土技術政策総合研究所より公表されていることが確認できた。
恐らくここに記載されている解析技術が
現時点のデファクトスタンダードであろう。
<出典:津波浸水想定の設定の手引 ver2.10 2019年4月>
https://www.mlit.go.jp/river/shishin_guideline/kaigan/tsunamishinsui_manual.pdf
当該資料によると、支配方程式について以下の記述がある。
津波のような長い周期の波に対してはその分散性が小さく長波理論が適用できる。従って、津波を推計する理論としては、だいたいの目安として 50m 以上の深海では線形長波理論、それ以下の浅海では非線形長波理論が用いられている。
、、、、、、??
ここで、線形長波理論/非線形長波理論について検索してみると、
”大林組技術研究所報"の津波の数値シミュレーション(津久井さん、藤澤さん)
の資料が見つかった。
線形長波理論/非線形長波理論の適用は、以下の考え方で良さそうだ。
津波の支配方程式
津波はその波長が数十kmから数百kmであるのに対して、
その発生した場所の水深は数kmであり、水深波長比は小さい。
このような波は長波と呼ばれ、鉛直方向の加速度を無視できる
近似が成立する。一方、波高水深比(波の非線形効果)は
津波が深海域であるが浅海域であるかによりその値は変化する。
津波の数値計算法は、これら波の特性を考慮して支配方程式を選択する。
式を書くのが面倒くさいので、以下に方程式に関する記載を転載する。
https://www.obayashi.co.jp/technology/shoho/057/1998_057_23.pdf
競艇場は数m程度の水深と思われるので
鉛直方向の加速度を無視してよいかは甚だ疑問であるが、、、
面倒なので、無視することにします。
ただし、波高水深比は考慮しておくか、、と。
よって、非線形長波理論なるものを支配方程式に適用することとした。
海モデルの構想2:解析手法(面倒なら飛ばしてください)
支配方程式が決定したので、具体的な解析手法の検討が必要だ。
競艇上は単純な四角形の形状をしているわけではないので、
精緻で安定的な物理シミュレーションを実施するためには、
一般座標系に変換することが必須だ。
(ざっくりと、、流れの方向に適した座標系に数式を変換する
必要がある、、。ぐらいで認識していただければと思います)
一般化座標に数式を直すのは、面倒である。
ここで、iricという河川の流れの解析ソフトに梱包されている
Nays2DH SolverManualなるものに、
よく似た方程式の一般座標(一般曲線座標)での計算式がのっていた。
これを参考に、非線形長波理論の一般曲線座標系への変換を行った。
計算式は、以下だ!!(たぶん)
<非線形長波理論:一般曲線座標系>
ここに
ざっと、tは時間、h'は静水面からの変動幅(波が動く高さ的な)、
Dは全水深、uが流速、gは重力加速度、ηとζが曲線座標の軸方向、
Jはヤコビアン、nは海面粗度係数
(津波シミュレーションで実測値に合わせるためのパラメータ的な)
という感じだ。細かい解説は面倒くさいので割愛したい。
そして、差分法は中心差分的な感じにした。
境界部は津波のマニュアルに反射させろ的なことが書いてあったので、
適当に反射させている。
海モデルの構想3:テスト計算結果
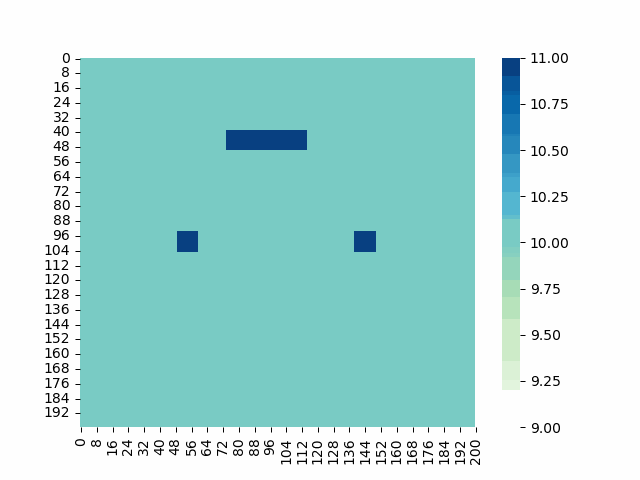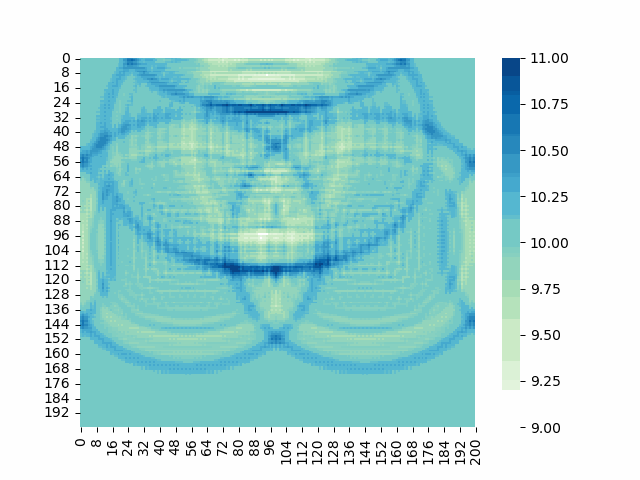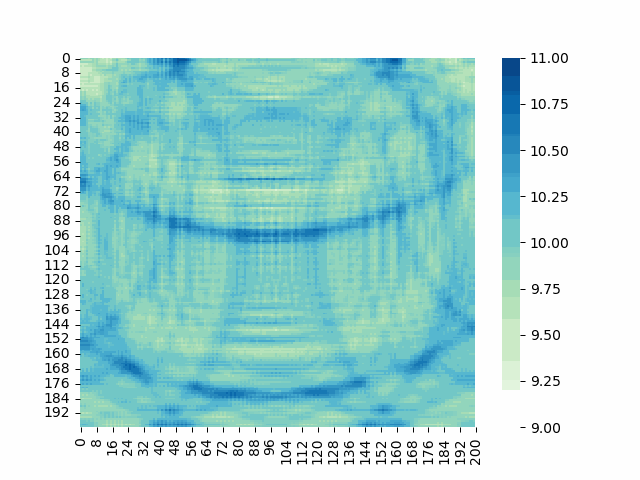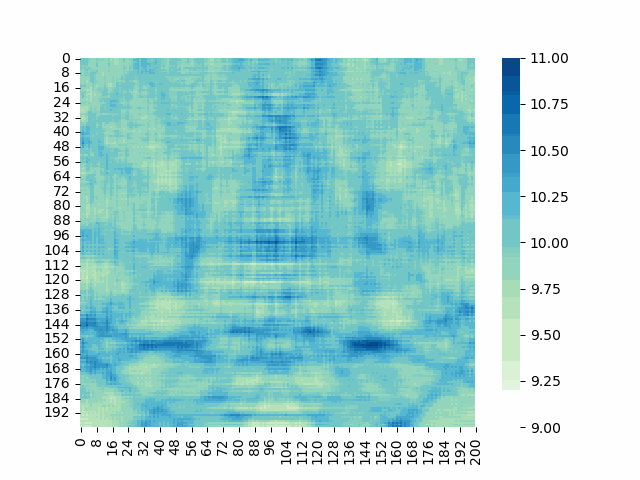
テストケースとして基本的に水位=10.0mの水面を作成し、
一部分だけ水位を1.0m加算した下図のような場を作成した。
さあ、これに対して海モデルによる計算をしてみよう!!
計算結果がこれだ!!(文頭にも載せてしまったが、、)

、、、、、、。

